Project Euler: Problem 15

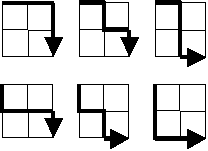
The next Euler problem is here:

Starting in the top left corner of a 2×2 grid, there are 6 routes (without backtracking) to the bottom right corner.

How many routes are there through a 20×20 grid?

This is one of the first interesting, non-trivial problems we’ve encountered so far, and subsequently this post will be slightly longer than usual. Also, note that although the problem description calls the grid in the example image a 2x2 grid, as far as the routers are concerned it’s for all intents and purposes just a 3x3 grid. Similarly, the 20x20 grid is actually a 21x21 grid when it comes to computing the possible routes.

Now, on to the solution. There are two key insights that will help get you there:

1. From all nodes along the right- and bottom edges of the grid, there is only one possible route towards the bottom-right corner: down or right in a straight line, respectively.
2. The number of possible routes to the bottom-right from each node can be defined recursively.

The first one is hopefully obvious enough not to go into further, so I’ll move on the the second one. The recursive definition I’m talking about can easily be derived from the following image:

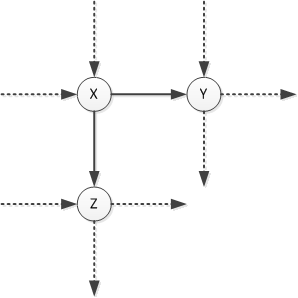
Let’s imagine you are in some position X, and you wonder how many possible routers there are towards the bottom-right corner. You have two options for movement: towards Y or towards Z. So how many routers does that give you? Well, however many routers there are starting from Y, plus how many there are starting from Z. Hence, we’ve arrived at the recursive definition: RoutesFrom(X) = RoutesFrom(Y) + RoutesFrom(Z).

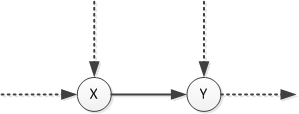
Of course, recall that if we end up at the right- or bottom (pictured) edge of the grid, only one option remains. So, in these cases, we get RoutesFrom(X) = 1.

We now have all the information we need to encode this problem in our favorite language (which is F#, obviously). The following function does the trick:

let rec PathsFrom(x, y, z) =
    if x = z || y = z then 1UL
    else PathsFrom(x + 1, y, z) + PathsFrom(x, y + 1, z)

It computes the number of possible paths starting at position (x, y) towards the bottom-right corner in a z-by-_z_ sized grid. We can call it as follows:

> PathsFrom(0, 0, 2);;

val it : uint64 = 6UL

>

And although the function does a fine job, it’s not very efficient. The number of paths also grows quite rapidly as the grid size increases: a 16x16 grid is still doable on my machine, but for the 17x17 grid computation time of all 2333606220 possible routes already approaches the one-minute mark, and it only gets worse from there.

So, let’s see if we can optimize this a little.

“Hey,” you might remark, “you said a 17x17 grid has 2333606220 possible routes, but there are only 18² = 324 different positions in the grid that you can move over!”

Very sharp of you. The obvious consequence is that each position in the grid is used by many, many different routes. However, the number of possible routes from each position is static. Yet in our current function, we freshly compute these values for each route. Seems like an awful waste, but luckily we have a fairly trivial solution: caching. The first time we arrive at a position, we compute the number of possible routes from there, and store this value for later use. Then, whenever we arrive at this position again on a different route, we can simply pull this value from the cache and be done with it.

Here’s the expanded function, with added caching:

open System.Collections.Generic

let rec NumPaths n =
    let cache = new Dictionary<(int * int), uint64>()
    let rec PathsFrom(x, y, z) =
        if x = z || y = z then 1UL
        else
            if cache.ContainsKey((x, y)) then cache.[(x, y)]
            elif cache.ContainsKey((y, x)) then cache.[(y, x)]
            else
                let m = PathsFrom(x + 1, y, z) + PathsFrom(x, y + 1, z)
                cache.Add((x, y), m)
                m
    PathsFrom(0, 0, n)

We use a dictionary as a cache with a position tuple as the key. Note that I optimize even further by using the symmetry of the grid: the number of routes from position (x, y) is the same as the number of routes from (y, x). We call this function as follows:

let result = NumPaths 20

This time, the answer is returned almost instantaneously.