Project Euler: Problem 18

Here’s another Euler problem for you!

By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.

3
7 4
2 4 6
8 5 9 3

That is, 3 + 7 + 4 + 9 = 23. Find the maximum total from top to bottom of the triangle below:

75
95 64
17 47 82
18 35 87 10
20 04 82 47 65
19 01 23 75 03 34
88 02 77 73 07 63 67
99 65 04 28 06 16 70 92
41 41 26 56 83 40 80 70 33
41 48 72 33 47 32 37 16 94 29
53 71 44 65 25 43 91 52 97 51 14
70 11 33 28 77 73 17 78 39 68 17 57
91 71 52 38 17 14 91 43 58 50 27 29 48
63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23

NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)

I have a feeling this will be interesting. And no, we won’t be brüte-forcing this one. We will be using C#. I’ve started by placing the large triangle in a text file, aligned like so:

75
95 64
17 47 82
18 35 87 10
20 04 82 47 65
19 01 23 75 03 34
88 02 77 73 07 63 67
99 65 04 28 06 16 70 92
41 41 26 56 83 40 80 70 33
41 48 72 33 47 32 37 16 94 29
53 71 44 65 25 43 91 52 97 51 14
70 11 33 28 77 73 17 78 39 68 17 57
91 71 52 38 17 14 91 43 58 50 27 29 48
63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23

We’ll then proceed to read the thing into an array:

var triangle = new int[15, 15];

using (var sr = new StreamReader("problem-18.txt"))
{
    for (int i = 0; i < 15; i++)
    {
        var line = sr.ReadLine().Split(' ');
        for (int j = 0; j < i + 1; j++)
        {
            triangle[i, j] = Int32.Parse(line[j]);
        }
    }
}

Just to be clear, the top of the triangle (value 75) is in position [0, 0] in the array, with [0, 1] to [0, 14] being empty. Now that we’ve got this high-tech datastructure set up, we can start solving the problem. We’ll do so by propagating all possible maximal paths down the tree, like so:

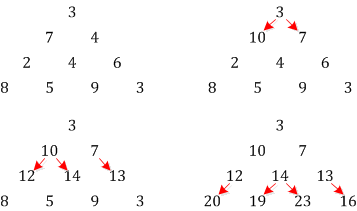
When we are on some layer, we need to propagate the largest possible values down to the layer below in order to continue the maximal path. In any of the nodes aside from those on the edges, this involves making a choice between the two nodes directly above it.

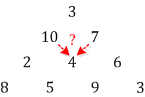
In the image above, we can get to the 4 node via a path leading trough the 10 node or a path leading through the 7 node. Obviously, the path leading through the 10 node results in the larger value, namely 14 versus 11 otherwise. So, when we propagate the maximal paths down the tree, every node ends up containing the sum of the maximal path leading up to it. In the general case, a propagation step of a layer i looks like the following:

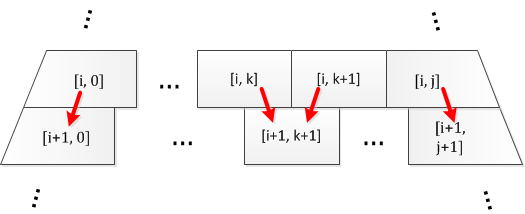
The two nodes on the edges, [i+1, 0] and [i+1, j+1], must take their values from the edge nodes of the layer above. For any of the nodes in between, there is a choice. Node [i+1, k+1] will take its value from either node [i, k] or [i, k+1] from the layer above. We will always choose whichever node has the highest value. The following code performs the propagation steps:

for (int i = 0; i < 14; i++)
{
    // next line, outer left
    triangle[i + 1, 0] += triangle[i, 0];

    // next line, outer right
    triangle[i + 1, i + 1] += triangle[i, i];

    for (int j = 0; j < i; j++)
    {
        // next line, shared child
        triangle[i + 1, j + 1] += Math.Max(triangle[i, j], triangle[i, j + 1]);
    }
}

When it is finished, the bottom nodes all contain the value of the maximal path leading up to it. Now all that remains is going through each one and finding the maximal value among them:

var max = 0;
for (int i = 0; i < 15; i++)
{
    if (triangle[14, i] > max)
        max = triangle[14, i];
}
Console.WriteLine(max);

This number is then the maximal total from top to bottom in the triangle.